A quick
search on Internet gives many references to DSLR
photometry. Amateur astronomers use DSLRs to observe stellar light curves
(see the AAVSO web
site) and to search for exoplanet transits, sometimes in the form of
amateur/professional collaborations (PANOPTES). There are also examples of the
use of DSLRs in the scientific literature: Velidovsky et al., used a Canon EOS 300D for absolute
photometry of the Moon.
Since I own
an old Canon EOS 300D I thought I’d try to measure a few fundamental
parameters: readout noise, dark current, and gain factors. The EOS 300D model
is now 10 years old and must be regarded as obsolete. I’ve seen them sold at
Ebay for less than 50 USD. It has a 12-bit 3088×2056 CMOS sensor, ISO settings
from 100 to 1600, exposure times from 0.25 milliseconds to 30 seconds, bulb
exposure of infinite length, but unfortunately no mirror lockup. I used IRIS to
convert files from RAW to FITS (note: without debayering the images), and IDL
for the actual analysis.
The gain
factors were determined by taking pairs of exposures from 0.25 to 100 milliseconds,
selecting a 600×400 pixel sub-frame, and plotting the variance of the
difference frame versus the mean level. Image
sequences were generated for ISO 400 and ISO 800, and the R-, G-, and
B-channels (of the Bayer matrix) were treated as independent data points. The
exposures were taken without lens, and with the camera pointed at a white,
uniformly lit wall. At first, the data points spread out across the graph but
when I discarded all exposures shorter than 10 milliseconds, the remaining data
points fell nicely along a straight line. For shorter exposure times, there is apparently
a large spread in the shutter performance (assuming that the light source is
constant between exposures). The uncertainty fell below 1% for exposure times
longer than around 50 milliseconds. This shutter performance may be a property
of the camera model, but it may also be a consequence of my camera being old
and worn-out.
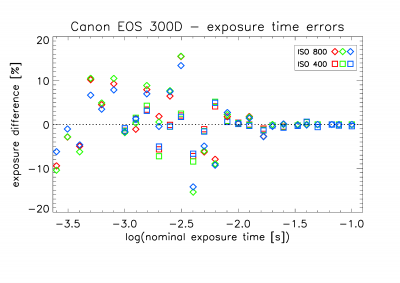
Figure 1. Percentage difference between pairs of exposures at different nominal exposure times.
The obtained
gain curves are shown in Figure 2. The resulting gain factors are g=2.58 electrons/ADU at ISO 400 and g=1.17 electrons/ADU at ISO 800,
which comply well with figures that I found at various web sites (here,
here). Above a signal level of around 3700
to 3800, the gain curves rapidly levels off to smaller noise values, indicating
an abrupt transition from linearity.
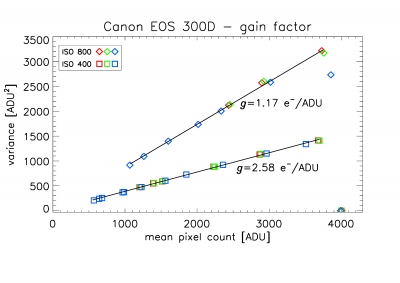
Figure 2. Variance of noise versus signal for ISO 400 and ISO 800.
Readout
noise and dark current was determined by repeating the above experiment, but now
with the camera body capped and going to exposure times longer than 20 minutes.
Figure 3 shows a surprising result: the dark current decreases with time, to levels below the CMOS bias level (128 for
the EOS 300D) which means negative values!
Clearly unphysical, but it could be explained as a consequence of
onboard dark-current subtraction before the CMOS frame hits the RAW file.
Apparently, the camera over-estimates the dark current. Or could it be IRIS
that does these subtractions in the RAW-to-FITS conversion?
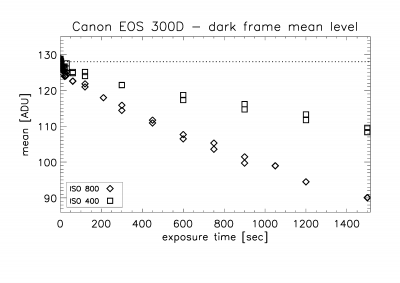 Figure 3. Dark current as a function of exposure time.
Figure 3. Dark current as a function of exposure time.
This behavior can only be
explained by onboard dark current subtraction before storage in the RAW file.
Even if the
dark current signal have been
subtracted in the RAW frame, the dark current noise is still there and this may tell us something about the dark
current signal. Figure 4 shows the dark
current variance as a function of exposure time. Up to 7 or 8 minutes it is a
roughly linear relation, but then the curve bends upwards – more strongly for
the ISO 800 sequence. The camera warms up during long exposures (one can
actually feel the temperature difference) and this is a likely explanation for
the nonlinear behavior in Figure 4. This is actually one of the major
limitations of DSLR cameras: the lack of temperature control causes a time
dependent behavior of the dark current, which is difficult to predict or to
monitor.
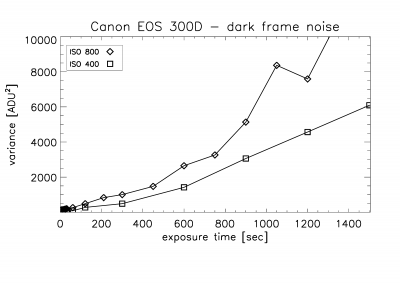
Figure 4. Dark current noise (here, the variance) as a
function of exposure time.
The readout noise can simply be obtained as the dark current for zero exposure
time. In Figure 5, we expand Figure 4 by plotting the logarithm of the observed
noise (but now the standard deviation) as a function of the logarithm of the
exposure time. Assuming that the observed noise is a combination of readout
noise and dark noise, and that the dark noise is proportional to the square
root of the exposure time (which it should be for exposures shorter than 5 to
10 minutes), we can fit both the readout noise and the dark current to the
observed data. Using the gain factors obtained above, we get a readout noise of
13.7 or 12.2 electrons, for ISO 400 and ISO 800, respectively, and a dark
current of about 3.6 electrons/pixel/second. This latter figure is highly uncertain,
but it suggests that for exposure times shorter than about 30 seconds the
readout noise dominates.
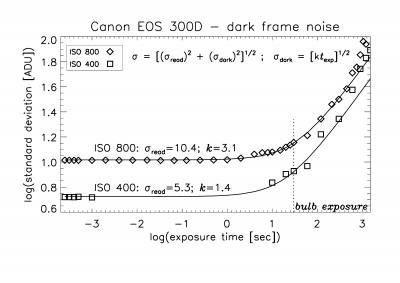
Figure 5. Dark current noise (here, the standard
deviation) versus exposure time on logarithmic scales.
Some
conclusions:
–
Gain
factors and readout noise obtained are relatively consistent with those found
by others. The dark current is a bit on the high side, but cannot be determined
very precisely.
–
The
camera shutter does not allow exposures shorter than 50 msec with any precision.
–
The
lack of temperature control makes the dark current unpredictable. This is less
of a problem for exposures shorter than 30-60 seconds, since they are dominated
by readout noise.
–
There
is some processing going on before the RAW file, at least a dark current
subtraction.
Even the least processed images – those in RAW formats – do not consist of the
raw, unprocessed data in the way we are used to from astronomical CCD cameras.
The details of this onboard processing are not described by the camera manufacturers. A
simple subtraction of a mean dark current level should not pose a problem for
the ability do photometry. However, if the processing includes scaling,
filtering, bad-pixel removal, “noise reduction”, etc., it may introduce
unpredictable errors in photometric measurements. How can we test this?

